Relación
Dados dos conjuntos A y B una relación es un subconjunto del producto cartesiano A x B.
Un elemento a, que pertenece al conjunto A, está relacionado con un elemento b, que pertenece al conjunto B, si el par (a, b) pertenece a un subconjunto G (llamado grafo) del producto cartesiano A x B.
Ejemplo: Sean A = {a, b, c} y B = {1, 2} dos conjuntos. El producto cartesiano A x B = {(a,1), (a,2), (b,1), (b,2), (c,1), (c,2)}. Una relación sería R = {(a,1),(c,2)}.
A las relaciones también se les llama correspondencias.
Considere dos conjuntos arbitrarios A y B. El conjunto de todas las parejas ordenadas (a, b) en donde a ∈ A y b ∈B se llama producto o producto cartesiano de A y B.
La definición de producto cartesiano puede extenderse fácilmente al caso de más de dos conjuntos.
Se llama producto cartesiano de dos conjuntos A y B y se representa A x B, al conjunto de pares ordenados (a, b), tales que el primer elemento pertenece al primer conjunto y el segundo elemento al segundo conjunto. Es decir:
A x B = {(a, b) / a ∈ A, b ∈ B} El producto cartesiano, en general, no es conmutativo. Es decir: A x B ≠ B x A.
Puede ocurrir que los conjuntos A y B sean coincidentes.
EJEMPLO:
Si A = {a, b, c} y B = {1, 2, 3, 4}, el producto cartesiano es:
A x B = {(a, 1), (a, 2), (a, 3), (a, 4), (b, 1), (b, 2), (b, 3), (b, 4), (c, 1), (c, 2), (c, 3), (c, 4)}
Se puede representar gráficamente por medio de puntos en un plano, como se muestra a continuación. Aquí, cada punto P representa una pareja ordenada (a, b) de números reales y viceversa; la línea vertical a través de P encuentra al eje x en a, y la línea horizontal a través de P encuentra el eje y en b.
A esta representación se le conoce como diagrama cartesiano.
Hay otra manera de visualizar una relación y es a través de una representación gráfica, donde se destaquen los puntos en el plano que pertenecen a A y los puntos que pertenecen a B. Se trazan flechas que indican la relación que existe entre cada elemento del conjunto A y su correspondiente en el conjunto B. A esta representación gráfica se le conoce como un diagrama de flechas.
Técnicas de Conteo.
Las técnicas de conteo son aquellas que son usadas para enumerar eventos difíciles de cuantificar.
Estas técnicas de conteo tienen como objetivo las combinaciones, estas se forman a través de 2 condiciones: con repetición y sin repetición, se pueden visualizar en forma de árboles,grupos y matriz (arreglo).
Empezaremos por explicar en que consiste el teorema fundamental de la multiplicación y de la adición..
Teorema Fundamental de la multiplicación: Si una combinación se quiere establecer de "n formas" y cada una de ellas se puede llevar a cabo de "m maneras distintas" en una segunda operación. Entonces se dice que juntas las operaciones pueden realizarse:nxm.
Ejemplo:
Se desea conocer el número de placas que se pueden formar si estas tienen 2 dígitos y 3 letras mayúsculas. Establecer de cuantas maneras se pueden formar sin repetición y con repetición.
Datos Dígitos (D) = 10
Letras mayúsculas (L)=27
Desarrollo
a)con repetición DDLLL = 10X10X27X27X27 = 1,968,300 maneras. b)sin repetición* DDLLL=10x9x27x26x25=1,579,500 maneras.
Teorema Fundamental de la Adición: Si un evento se puede llevar a cabo de "n o m lugares distintos", además de no ser posible que se lleve a cabo el mismo evento o dos lugares distinto al mismo tiempo. Entonces el evento se puede realizar: n+m formas diferentes.
Ejemplo
Supóngase que se desea etiquetar las gavetas de los alumnos de la primaria, y que la etiqueta puede estar marcada con un solo digito, una sola letra o la combinación de una sola letra con un solo digito (sin importar si primero se pone la letra y después el digito o al contrario. *Bajo estas condiciones , el numero de etiquetas distintas que se pueden formar son:
Datos
D=10
L=27
Desarrollo
Etiquetas= D+L+D*L+L*D al sustituir queda:
Etiquetas=10+27+10*27+27*10
Etiquetas=577
a)con repetición DDLLL = 10X10X27X27X27 = 1,968,300 maneras. b)sin repetición* DDLLL=10x9x27x26x25=1,579,500 maneras.
Teorema Fundamental de la Adición: Si un evento se puede llevar a cabo de "n o m lugares distintos", además de no ser posible que se lleve a cabo el mismo evento o dos lugares distinto al mismo tiempo. Entonces el evento se puede realizar: n+m formas diferentes.
Ejemplo
Supóngase que se desea etiquetar las gavetas de los alumnos de la primaria, y que la etiqueta puede estar marcada con un solo digito, una sola letra o la combinación de una sola letra con un solo digito (sin importar si primero se pone la letra y después el digito o al contrario. *Bajo estas condiciones , el numero de etiquetas distintas que se pueden formar son:
Datos
D=10
L=27
Desarrollo
Etiquetas= D+L+D*L+L*D al sustituir queda:
Etiquetas=10+27+10*27+27*10
Etiquetas=577
Permutaciones
Hay dos tipos de permutaciones:
- Se permite repetir: como la cerradura de arriba, podría ser "333".
- Sin repetición: por ejemplo los tres primeros en una carrera. No puedes quedar primero y segundo a la vez.
1. Permutaciones con repetición
Son las más fáciles de calcular. Si tienes n cosas para elegir y eliges r de ellas, las permutaciones posibles son:
n × n × ... (r veces) = nr
(Porque hay n posibilidades para la primera elección, DESPUÉS hay n posibilidades para la segunda elección, y así.)
Por ejemplo en la cerradura de arriba, hay 10 números para elegir (0,1,...,9) y eliges 3 de ellos:
10 × 10 × ... (3 veces) = 103 = 1000 permutaciones
Así que la fórmula es simplemente:
| nr |
| donde n es el número de cosas que puedes elegir, y eliges r de ellas (Se puede repetir, el orden importa) |
2. Permutaciones sin repetición
En este caso, se reduce el número de opciones en cada paso.
 |
Por ejemplo, ¿cómo podrías ordenar 16 bolas de billar?
Después de elegir por ejemplo la "14" no puedes elegirla otra vez.
|
Así que tu primera elección tiene 16 posibilidades, y tu siguiente elección tiene 15 posibilidades, después 14, 13, etc. Y el total de permutaciones sería:
16 × 15 × 14 × 13 ... = 20,922,789,888,000
Pero a lo mejor no quieres elegirlas todas, sólo 3 de ellas, así que sería solamente:
16 × 15 × 14 = 3360
Es decir, hay 3,360 maneras diferentes de elegir 3 bolas de billar de entre 16.
¿Pero cómo lo escribimos matemáticamente? Respuesta: usamos la "función factorial"
 |
La función factorial (símbolo: !) significa que se multiplican números descendentes. Ejemplos:
|
| Nota: en general se está de acuerdo en que 0! = 1. Puede que parezca curioso que no multiplicar ningún número dé 1, pero ayuda a simplificar muchas ecuaciones. | |
Así que si quieres elegir todas las bolas de billar las permutaciones serían:
16! = 20,922,789,888,000
Pero si sólo quieres elegir 3, tienes que dejar de multiplicar después de 14. ¿Cómo lo escribimos? Hay un buen truco... dividimos entre 13!...
16 × 15 × 14 × 13 × 12 ...
| = 16 × 15 × 14 = 3360 | |
13 × 12 ...
|
¿Lo ves? 16! / 13! = 16 × 15 × 14
La fórmula se escribe:
| donde n es el número de cosas que puedes elegir, y eliges r de ellas (No se puede repetir, el orden importa) |
Ejemplos:
Nuestro "ejemplo de elegir en orden 3 bolas de 16" sería:
| 16! | = | 16! | = | 20,922,789,888,000 | = 3360 |
| (16-3)! | 13! | 6,227,020,800 |
¿De cuántas maneras se pueden dar primer y segundo premio entre 10 personas?
| 10! | = | 10! | = | 3,628,800 | = 90 |
| (10-2)! | 8! | 40,320 |
(que es lo mismo que: 10 × 9 = 90)
Combinaciones
También hay dos tipos de combinaciones (recuerda que ahora el orden no importa):
- Se puede repetir: como monedas en tu bolsillo (5,5,5,10,10)
- Sin repetición: como números de lotería (2,14,15,27,30,33)
1. Combinaciones sin repetición
Así funciona la lotería. Los números se eligen de uno en uno, y si tienes los números de la suerte (da igual el orden) ¡entonces has ganado!
La manera más fácil de explicarlo es:
- imaginemos que el orden sí importa (permutaciones),
- después lo cambiamos para que el orden no importe.
Volviendo a las bolas de billar, digamos que queremos saber qué 3 bolas se eligieron, no el orden.
Ya sabemos que 3 de 16 dan 3360 permutaciones.
Pero muchas de ellas son iguales para nosotros, porque no nos importa el orden.
Por ejemplo, digamos que se tomaron las bolas 1, 2 y 3. Las posibilidades son:
| El orden importa | El orden no importa |
| 1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1 | 1 2 3 |
Así que las permutaciones son 6 veces más posibilidades.
De hecho hay una manera fácil de saber de cuántas maneras "1 2 3" se pueden ordenar, y ya la sabemos. La respuesta es:
3! = 3 × 2 × 1 = 6
(Otro ejemplo: 4 cosas se pueden ordenar de 4! = 4 × 3 × 2 × 1 = 24 maneras distintas, ¡prueba tú mismo!)
Así que sólo tenemos que ajustar nuestra fórmula de permutaciones para reducir por las maneras de ordenar los objetos elegidos (porque no nos interesa ordenarlos):
Esta fórmula es tan importante que normalmente se la escribe con grandes paréntesis, así:
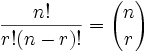 |
| donde n es el número de cosas que puedes elegir, y eliges r de ellas (No se puede repetir, el orden no importa) |
Y se la llama "coeficiente binomial".
Notación
Además de los "grandes paréntesis", la gente también usa estas notaciones:
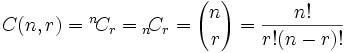
Ejemplo
Entonces, nuestro ejemplo de bolas de billar (ahora sin orden) es:
| 16! | = | 16! | = | 20,922,789,888,000 | = 560 |
| 3!(16-3)! | 3!×13! | 6×6,227,020,800 |
O lo puedes hacer así:
| 16×15×14 | = | 3360 | = 560 |
| 3×2×1 | 6 |
Así que recuerda, haz las permutaciones, después reduce entre "r!"
... o mejor todavía...
¡Recuerda la fórmula!
Es interesante darse cuenta de que la fórmula es bonita y simétrica:
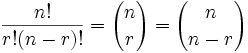
Con otras palabras, elegir 3 bolas de 16 da las mismas combinaciones que elegir 13 bolas de 16.
| 16! | = | 16! | = | 16! | = 560 |
| 3!(16-3)! | 13!(16-13)! | 3!×13! |
. Combinaciones con repetición
OK, ahora vamos con este...
 |
Digamos que tenemos cinco sabores de helado: banana, chocolate, limón, fresa y vainilla. Puedes tomar 3 paladas. ¿Cuántas variaciones hay?
Vamos a usar letras para los sabores: {b, c, l, f, v}. Algunos ejemplos son
|
(Y para dejarlo claro: hay n=5 cosas para elegir, y eliges r=3 de ellas.
El orden no importa, ¡y sí puedes repetir!)
El orden no importa, ¡y sí puedes repetir!)
Bien, no puedo decirte directamente cómo se calcula, pero te voy a enseñar una técnica especial para que lo averigües tú mismo.
Imagina que el helado está en contenedores, podrías decir "sáltate el primero, después 3 paladas, después sáltate los 3 contenedores siguientes" ¡y acabarás con 3 paladas de chocolate!
| |
| Entonces es como si ordenaras a un robot que te trajera helado, pero no cambia nada, tendrás lo que quieres. |
Ahora puedes escribirlo como  (la flecha es saltar, el círculo es tomar)
(la flecha es saltar, el círculo es tomar)
Entonces los tres ejemplos de arriba se pueden escribir así:
| {c, c, c} (3 de chocolate): | |
| {b, l, v} (uno de banana, uno de limón y uno de vainilla): | |
| {b, v, v} (uno de banana, dos de vainilla): |
OK, entonces ya no nos tenemos que preocupar por diferentes sabores, ahora tenemos un problema más simple para resolver: "de cuántas maneras puedes ordenar flechas y círculos"
Fíjate en que siempre hay 3 círculos (3 paladas de helado) y 4 flechas (tenemos que movernos 4 veces para ir del contenedor 1º al 5º).
Así que (en general) hay r + (n-1) posiciones, y queremos que r de ellas tengan círculos.
Esto es como decir "tenemos r + (n-1) bolas de billar y queremos elegir r de ellas". Es decir, es como el problema de elegir bolas de billar, pero con números un poco distintos. Lo podrías escribir así:
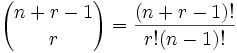 |
| donde n es el número de cosas que puedes elegir, y eliges r de ellas (Se puede repetir, el orden no importa) |
Es interesante pensar que podríamos habernos fijado en flechas en vez de círculos, y entonces habríamos dicho "tenemos r + (n-1) posiciones y queremos que (n-1) tengan flechas", y la respuesta sería la misma...
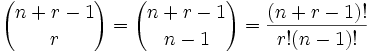
¿Qué pasa con nuestro ejemplo, cuál es la respuesta?
| (5+3-1)! | = | 7! | = | 5040 | = 35 |
| 3!(5-1)! | 3!×4! | 6×24 |



No hay comentarios:
Publicar un comentario