Supóngase que una sucesión S de n objetos tien n1 objetos idénticos del tipo 1, n2 objetos idénticos del tipo 2, . . . , nt objetos idénticos del tipo t. Entonces el número de ordenaciones de S es:
Demostración:
Se asignan las posiciones de cada uno de los n objetos para crear un orden de S. Es posible asignar las posiciones de los n1 objetos del tipo 1 en C(n, n1) formas. Una vbez realizada estas asignación, pueden asignarse las posiciones de los n2 objetos del tipo 2 en C(n - n1, n2) maneras, etc. Por lo tanto
Se asignan las posiciones de cada uno de los n objetos para crear un orden de S. Es posible asignar las posiciones de los n1 objetos del tipo 1 en C(n, n1) formas. Una vbez realizada estas asignación, pueden asignarse las posiciones de los n2 objetos del tipo 2 en C(n - n1, n2) maneras, etc. Por lo tanto
coeficientes binomial
Los coeficientes binomiales, números combinatorios o combinaciones son números estudiados en combinatoria que corresponden al número de formas en que se pueden extraer subconjuntos a partir de un conjunto dado. Sin embargo, dependiendo del enfoque que tenga la exposición, se pueden usar otras definiciones equivalentes.
Ejemplo:
Se tiene un con 6 objetos diferentes {A,B,C,D,E,F}, de los cuales se desea escoger 2
(sin importar el orden de elección). Existen 15 formas de efectuar tal
elección:
A,B
|
A,C
|
A,D
|
A,E
|
A,F
|
B,C
|
B,D
|
B,E
|
B,F
|
|
C,D
|
C,E
|
C,F
|
||
D,E
|
D,F
|
|||
E,F
|
El número de formas de escoger k elementos a partir de un conjunto de n, puede denotarse de varias formas C(n,k), n,Ck. Así, en el
ejemplo anterior se tiene entonces que C(6,2)=15, puesto que hay 15 formas de
escoger 2 objetos a partir de un conjunto con 6 elementos.
Los números C(n,k) se
conocen como «coeficientes binomiales»,
pero es frecuente referirse a ellos como «combinaciones de n en k», o simplemente «n en k». Por tanto, la
primera definición es:
El coeficiente binomial es el
número de subconjuntos de k elementos escogidos de un conjunto con n elementos.
|
Es importante notar que la
definición asume implícitamente que n y k son naturales, y que además k no excede a n. Podemos definir C(n,k)=0
si k>n,
puesto que no es posible escoger más elementos que los que tiene el conjunto
dado (por tanto hay cero formas
de hacer la elección). Estas precisiones cobrarán relevancia más adelante
cuando se discutan generalizaciones del concepto (por ejemplo, cuando n o k sean negativos o cuando no
sean números enteros).
Aplicación al análisis de algoritmos
La resolución práctica de un problema exige por una parte un algoritmo o método de resolución y por otra un programa o codificación de aquel en un ordenador real. Ambos componentes tienen su importancia; pero la del algoritmo es absolutamente esencial, mientras que la codificación puede muchas veces pasar a nivel de anécdota.
A efectos prácticos o ingenieriles, nos deben preocupar los recursos físicos necesarios para que un programa se ejecute. Aunque puede haber muchos parametros, los mas usuales son el tiempo de ejecución y la cantidad de memoria (espacio). Ocurre con frecuencia que ambos parametros están fijados por otras razones y se plantea la pregunta inversa: ¿cual es el tamano del mayor problema que puedo resolver en T segundos y/o con M bytes de memoria? En lo que sigue nos centraremos casi siempre en el parametro tiempo de ejecución, si bien las ideas desarrolladas son fácilmente aplicables a otro tipo de recursos.Para cada problema determinaremos un medida N de su tamaño (por número de datos) e intentaremos hallar respuestas en función de dicho N. El concepto exacto que mide N depende de la naturaleza del problema. Así, para un vector se suele utizar como N su longitud; para una matriz, el número de elementos que la componen; para un grafo, puede ser el número de nodos (a veces es mas importante considerar el número de arcos, dependiendo del tipo de problema a resolver); en un fichero se suele usar el número de registros, etc. Es imposible dar una regla general, pues cada problema tiene su propia lógica de coste.
Tipos de ejecucion
Una medida que suele ser útil conocer es el tiempo de ejecución de un programa en función de N, lo que denominaremos T(N). Esta función se puede medir físicamente (ejecutando el programa, reloj en mano), o calcularse sobre el código contando instrucciones a ejecutar y multiplicando por el tiempo requerido por cada instrucción. Así, un trozo sencillo de programa como
S1; for (int i= 0; i < N; i++) S2;
requiere T(N)= t1 + t2*N
siendo t1 el tiempo que lleve ejecutar la serie "S1" de sentencias, y t2 el que lleve la serie "S2".Prácticamente todos los programas reales incluyen alguna sentencia condicional, haciendo que las sentencias efectivamente ejecutadas dependan de los datos concretos que se le presenten. Esto hace que mas que un valor T(N) debamos hablar de un rango de valores
Tmin(N) <= T(N) <= Tmax(N)
los extremos son habitualmente conocidos como "caso peor" y "caso mejor". Entre ambos se hallara algun "caso promedio" o más frecuente.Cualquier fórmula T(N) incluye referencias al parámetro N y a una serie de constantes "Ti" que dependen de factores externos al algoritmo como pueden ser la calidad del código generado por el compilador y la velocidad de ejecución de instrucciones del ordenador que lo ejecuta. Dado que es fácil cambiar de compilador y que la potencia de los ordenadores crece a un ritmo vertiginoso (en la actualidad, se duplica anualmente), intentaremos analizar los algoritmos con algun nivel de independencia de estos factores; es decir, buscaremos estimaciones generales ampliamente válidas.
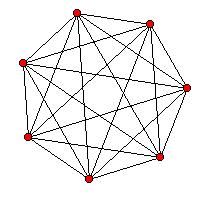
Grafos
De esta manera podemos dejar patente que aquel emana de la palabra griega grafo, graphein, que puede traducirse como “grabar o escribir”.
 Este hecho es el que determina, por ejemplo, que hoy día utilicemos dicho concepto como
Este hecho es el que determina, por ejemplo, que hoy día utilicemos dicho concepto como
En la lingüística, un grafo es un objeto unitario de naturaleza abstracta que abarca a las grafias que componen una letra. La palabra tiene origen griego y significa “imagen ” o “dibujo”.
Los grafos pueden ser clasificarse de diversas maneras según sus características. Los grafos simples, en este sentido, son aquellos que surgen cuando una única arista logra unir dos vértices. Los grafos complejos, en cambio , presentan más de una arista en unión con los vértices.
Por otra parte, un grafo es conexo si dispone de dos vértices conectados a través de un camino. ¿Qué quiere decir esto? Que, para el par de vértices (p, r), tiene que existir algún camino que permita llegar desde p hasta r.
En cambio, un grafo es fuertemente conexo si el par de vértices tiene conexión a través de, como mínimo, dos caminos diferentes.
Un grafo simple, además, puede ser completo si las aristas están en condiciones de unir todos los pares de vértices, mientras que un grafo es bipartito si sus vértices surgen por la unión de un par de conjuntos de vértices y si se cumple una serie de condiciones.
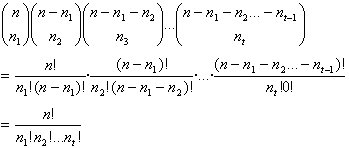
No hay comentarios:
Publicar un comentario